Co je tepelný stroj
V praxi jste se setkáváli, setkáváte a určitě se budete setkávat se stroji. Celá řada z nich jsou tzv. stroje tepelné. Mohou to být například motor v automobilu, tryskový motor ve stíhačce, turbína, atd.
pohled na motor v autě
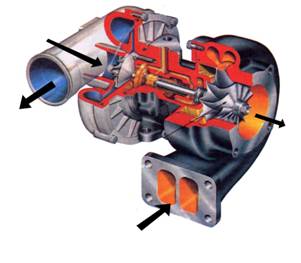
turbodmychadlo
Tyto stroje pracují tak, že nějakým způsobem přebírají teplo z teplého zásobníku a přemění jej na práci. Díky tomu mohou automobily jezdit, stíhačky létat, elektrárny vyrábět elektřinu (a příroda trpí 
, ale když jezdit na kole je tak namáhavé).
schéma tepelného stroje
Nyní vás bude jistě zajímat, za jakých okolností mohou automobily jezdit, stíhačky létat a elektrárny vyrábět elektrický proud. Určitě by vás nepotěšilo, kdyby se auto najednou zastavilo a dál nejelo, u stíhačky by byl tento problém fatální a zkuste mluvit na svou babičku uprostřed její oblíbené telenovely, když jí vypnou proud. Co se této otázky týče, odpověď na ni dal mladý francouzský vojenský inženýr Nicolas Léonard Sadi Carnot již v první čtvrtině 19. století.
Ten došel k závěru, že teplo může, např. v parním stroji, konat práci jen tehdy, jestliže může samovolně přecházet. A to se děje jedině z tělesa teplejšího na chladnější. Například vy se ohřejete od teplých kamen, kdežto kamna se od vás neohřejí. Pro konání práce nějakým tepelným strojem tedy nestačí mít jen těleso nebo obecně látku o určité teplotě, která práci koná, musí být k dispozici druhé těleso o vhodné nižší teplotě, které teplo přijímá. Carnot vyšel ze zdánlivé podobnosti mezi teplem a vodou tekoucí z vyšší polohy do nižší.
Takže proto musí horká pára z kotle parního stroje odcházet ven do okolí, které v tomto případě představuje chladnou lázeň stejně jako v případě výfuků u automobilů, u chladících věží elektráren, atd.
Clausiova formulace
Právě fakt, že těleso nemůže přecházet z tělesa chladnějšího na těleso teplejší je obsahem Clausiovy formulace 2. věty termodynamiky.
Clausiova formulace (1850): Teplo nemůže samovolně přecházet z tělesa studenějšího na těleso teplejší.
V předchozím odstavci bylo zmíněno, že teplo z teplejšího zásobníku je přeměňováno na práci. Ovšem další důležitá otázka zní: Jste schopni přeměnit všechno teplo z teplejšího zásobníku na práci a pokud ano, tak jak? A pokud nikoliv, jakou část jste schopni přeměnit na práci a jak to učinit, aby tato část byla co největší?
Pro zodpovězení této otázky bude vhodné zavést pojem účinnost. Ta vám říká, kolik tepla přeměníte na práci z celkové energie, kterou stroji dodáte ve formě tepla, tedy
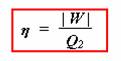
Účinnost značíme řeckým písmenem 
[éta] a nemá žádné jednotky, je to tedy bezrozměrná veličina. Nejčastěji se účinnost uvádí v % (to je číslo, které vám vyjde z uvedeného vztahu vynásobené 100). Tedy například účinnost 30% znamená, že dodáte-li stroji 100 J, 30 J stroj odevzdá jako práci, dodáte-li 50 J, 15 J stroj vykoná jako práci.
Dále se pokusíme odvodit, zda je možné veškeré teplo dodané stroji přeměnit na práci. Ještě jednou se podívejte na schéma tepelného stroje. Z obrázku je patrné, že výsledná práce W vykonaná strojem je rovna rozdílu Q2 (teplo dodané teplejším zásobníkem) a Q1 (teplo odevzdané okolí), tedy W = Q2 – Q1. Z toho vyplývá, že vztah pro účinnost lze napsat následovně:
Pomocí tzv. Carnotova cyklu zjistíme, že účinnost lze vypočítat podle následujícího vztahu:
Tzn., že čím vyšší rozdíl v čitateli a čím nižší teplota T2, tím vyšší účinnost. Nicméně, vzhledem k tomu, že dosažení absolutní nuly je nemožné (alespoň se to dosud nikomu nepodařilo), tak nikdy nebude čitatel vyšší nebo roven jmenovateli, a proto účinnost nemůže být rovna nebo vyšší než 100 %, a to i v případě, že by stroj pracoval absolutně bez tření a jakýchkoliv jiných energetických ztrát. Za běžných podmínek, kdy teplejší zásobník má okolo 100 °C (parní stroj) až 2000 °C (tryska ze stíhačky) a chladnějším zásobníkem je okolí lze snadno vypočítat, že účinnost tepelného stroje bez jakýchkoliv jiných energetických ztrát činí
Skutečná účinnost často bývá podstatně nižší díky tření a jiným energetickým ztrátám (třeba 1/3 nebo až 1/10 vypočítané hodnoty). Pokud by se vám podařilo sestavit stroj, jehož účinnost by byla vyšší než ona vypočítaná, gratulovali bychom vám, právě se vám podařilo sestavit perpetuum mobile II. druhu a porušujete 2. zákon termodynamiky 
. Z toho vyplývá i druhá formulace 2. věty termodynamiky vyřčená W. Thomsonem.
Thomsonova formulace
Thomsonova formule (1851):
Nelze sestrojit perpetuum mobile II. druhu (nelze beze zbytku přeměňovat cyklicky teplo na práci). Tedy nemůžete vyrobit takový stroj, který by konal práci a veškerou svoji energii by přeměnil na práci.
Na základě řečeného se pokuste odpovědět na následující otázku:
Jestliže spalovací motor přeměňuje tepelnou energii v mechanickou energii („teplo v práci“), je zřejmé, že výfuk spalin představuje ztrátu tepla. Bylo by možné jí zabránit (přeměnit i toto teplo v práci)?
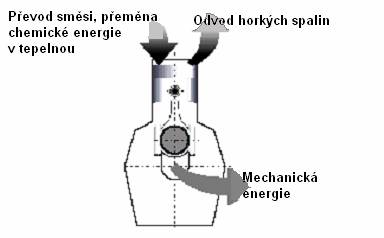
citováno z: http://www.spstrplz.cz/osobnistranky/josef_gruber/td/td_learn.pdf
Odpověď na otázku:
Pokud byste znemožnili odvod odpadního tepla ze stroje, stroj by se přehřál. Odpadní teplo nevyužijete pro užitečnou práci, protože jej nese látka, která má teplotu blízkou okolí a v okolí se nenachází jiná látka o nižší teplotě, na níž by ono teplo mohlo přejít. Z tohoto důvodu nelze využít např. velké množství tepla v okolním vzduchu, které je uchováváno při nízké teplotě a není k dispozici vhodná nižší teplota.
Budete chápat 2. termodynamický zákon jako zákon, který zkoumá, kolik tepla přijatého od okolí (tepelná lázeň) může soustava (tepelný stroj) přeměnit na práci.
Samovolné děje
Určitě jste si někdy všimli, že jsou děje, které probíhají samovolně a naopak děje které probíhají nesamovolně. Nejprve se zkusíme podívat na následující obrázky.
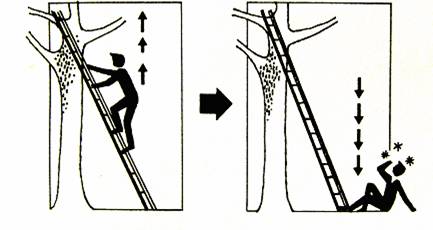
Člověk stojící na žebříku může kdykoliv spadnout na zem, ale nikdy se nemůže „vznést“ ze země na žebřík.
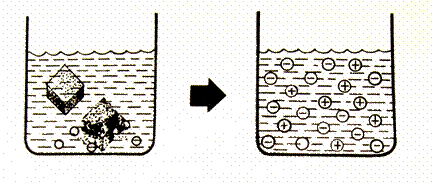
Některé látky se snadno rozpustí ve vodě, ale nikdy se neoddělí bez dodání energie látky z vody.
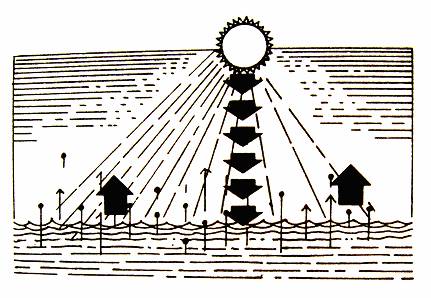
Za suchého dne se kaluže vody rychle vypaří, ale nikdy se za těchto podmínek neuskuteční děj opačný.
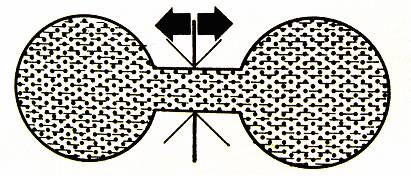
Dva plyny se po otevření záklopky smísí, ale nikdy se dva plyny od sebe samovolně neoddělí.
Často dovedete odhadnout, kterým směrem děje budou probíhat a kterým směrem bude třeba dodat energii (např. je nám jasné, že na žebřík se nikdy samovolně nevznesete, zatímco samovolný pád je dílem okamžiku při chvilce nepozornosti). Jsou ale děje, kdy onen odhad, daný většinou naší zkušeností, tak jednoduchý není. Často je tomu u některých chemických reakcí, zvláště těch, které ještě nikdo nevyzkoušel. Například reakce vodíku s jodem. Bude spíše vznikat jodovodík z obou prvků nebo naopak se bude jodovodík rozkládat na prvky? Tady už není odpověď tak jednoznačná a asi jen málokdo z vás dokáže s jistotou říci, jak a kterým směrem bude tato reakce probíhat. A to je dalším velice důležitým úkolem termodynamiky. Proč a za jakých podmínek probíhají děje samovolně (tedy bez vnějšího přispění energie), proč probíhají přeměny některých látek v produkty a proč naopak jiné látky za těchto podmínek spolu nereagují. Praktické důsledky jsou zřejmé. Jsou-li například reaktanty velice drahé, bude vás zajímat, jestli nejde nějakým způsobem předpovědět průběh reakce, abyste ji nemuseli provádět a utratit spoustu peněz s nulovým výsledkem. Dále, máte-li podezření, že daná reakce bude probíhat explozivně, je opět vhodné udělat předem termodynamické výpočty, abyste poté nepřekvapili sousedy nečekanou explozí. K tomu, abyste mohli provést daný odhad, potřebujete jakési kritérium. Tím kritériem (a časem se ukáže, že ne jediným) pro vás bude entropie S. Nicméně ona entropie vám nespadne z nebe. Všimněte si náhodné spojitosti s pečenými holuby, kteří také sami nelétají do úst. Proto si budeme muset entropii odvodit. To ovšem vyžaduje hlubší matematické znalosti z oblasti diferecniálního a integrálního počtu, a tak je toto odvození dostupné pouze hrstce vyvolených. Ostatní, nevyvolení, se spokojí s tvrzením, které ono náročné odvození poskytuje, totiž že v adiabaticky izolované soustavě roste entropie tak dlouho, dokud se soustava nedostane do rovnováhy. V rovnováze, kdy mohou probíhat jen vratné děje, je entropie soustavy maximální. Bude-li tedy v adiabaticky izolované soustavě probíhat děj, který je samovolný, musí entropie soustavy růst, tzn. ΔS > 0. To můžeme i obrátit. Pokud má být v adiabaticky izolované soustavě děj samovolný, musí být ΔS > 0. V případě, že ΔS = 0, systém je v rovnováze a probíhají pouze vratné děje. Hodnoty entropií pro dané podmínky (většinou standardní stav) můžete nalézt v tabulkách. V případě, že je ΔS < 0, děj nebude probíhat samovolně. Pro lepší názornost jsme vám tu situaci zpříjemnili tabulkou. Bohužel je ale pravda, že entropie je vhodným kritériem pouze pro soustavy adiabaticky izolované, na druhé straně je to lepší než dostat drátem do oka . Navíc, zanedlouho se dozvíte, že pro jiné podmínky (izotermicko-izobarické, atd.) máte jiná kritéria (Gibbsova funkce, Helmholtzova funkce).
Entropie jako kritérium v adiabaticky izolované soustavě:
ΔS > 0 |
děj bude samovolný |
ΔS = 0 |
probíhají pouze vratné děje (systém může být v rovnováze) |
ΔS < 0 |
děj nebude probíhat samovolně (děj je nesamovolný) |
Entropie
(z řec. éntrépein = obraceti)
K entropii se lze dostat přes účinnost. Účinnost jsme si zadefinovali následovně.
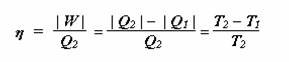
Vzhledem k tomu, že tepelný stroj teplo i práci do okolí odevzdává, má Q1 i W ve skutečnosti záporné znaménko a Q2 je teplo stroji dodané, má znaménko kladné. Pak můžete psát :
Tento vztah platí pouze pro reverzibilní děje. Pro děj ireverzibilní je ovšem účinnost vždy nižší než pro děj reverzibilní (to plyne například z Carnotova cyklu). Pro ireverzibilní děje můžete tedy psát, že
.
A pro reverzibilní děj můžete napsat
.
Dohromady platí
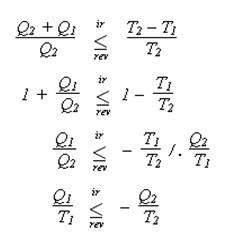
Po pár jednoduchých matematických úpravách se nakonec dostanete k:
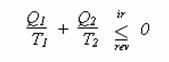
Opět pan Carnot dokázal, že poněkud sofistikovaným postupem lze odvodit v podstatě totéž pro komplikovanější stroj pracující mezi libovolným počtem n lázní o teplotách T1, … ,Tn .
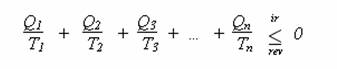
Což lze matematicky zapsat stručněji:
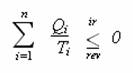
Matematická formulace
Protože pan Carnot byl znalý diferenciálního a integrálního počtu, odvodil pro případ, že se teplota lázní mění spojitě (tj. teplota sousedících si lázní se liší o velmi malou neměřitelnou část), následující vztah, jehož se nelekejte:
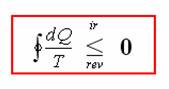
Tento výraz je matematickou formulací 2. termodynamické věty.
Symbol 
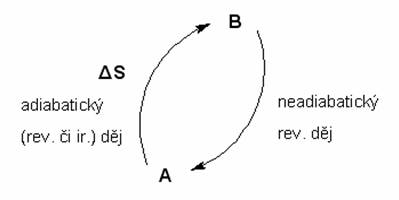
značí kruhový integrál. Ten v podstatě přikazuje integrovat (sčítat) všechny přírůstky pro přechod systému po kruhové cestě z určitého stavu zpět do téhož stavu. V podstatě jde o integrál ze stavu A do stavu A 
, přičemž ale ve stavu A je systém pouze na začátku a na konci děje. Pro lepší názornost následující obrázek (i když matematici nás za něj ukamenují).
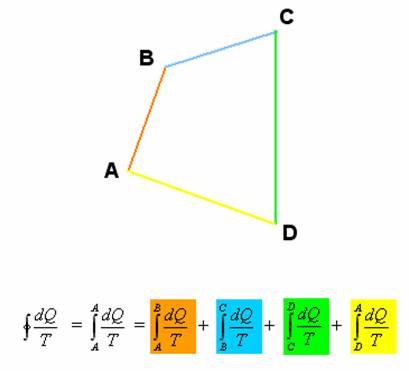
Výraz je pro reverzibilní cyklický děj tzv. totálním (úplným) diferenciálem. Pro vysvětlení totálního diferenciálu je nutná znalost vyšší matematiky. Ale představte si funkci dvou reálných proměnných (například x a y). Jestliže je funkce diferencovatelná, neboli má totální diferenciál, zároveň musí splňovat dvě podmínky. Za prvé: v okolí bodu musí existovat parciální (částečné) derivace obou proměnných a zároveň, a to je druhá podmínka, tyto derivace jsou spojité. Pro jednoduchost, spojitost znamená, že se funkce dá nakreslit „jedním tahem“. Správně bychom měli tyto pojmy pořádně vysvětlit, ale vy se spokojíte s touto definicí, neboť vás zajímá chemická podstata věci nikoliv matematické odvozování . Jejich důležitou vlastností je, že kruhový integrál totálního diferenciálu je roven nule.
Pomocí totálního diferenciálu zavedeme novou stavovou funkci, která se nazývá entropie, značí se S. Entropie je definována následující rovnicí:
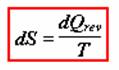
Integrací uvedeného výrazu pro děj provedený za izotermických podmínek:
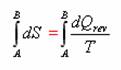
Jedná se tedy o diferenciální rovnici, kterou budeme řešit separací proměnných.
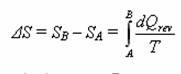
Převedete-li systém ze stavu A do stavu B a to adiabaticky (ať už vratně nebo nevratně) (
) a následně zpět do stavu A vratně (
). Podle 2. věty termodynamiky lze psát :
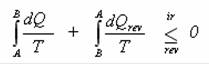
Jak jsme si již říkali, přechod ze stavu A do stavu B je adiabatický, takže dQ = 0 a celý první člen tedy vypadne. Zbyde vám následující vztah
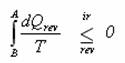
Všimněte si nápadné podobnosti s výrazem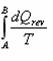 
ze vztahu 
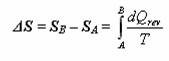, uvedeného o 9 řádků výše. Pro znalce integrálního počtu a z toho důvodu, že entropie je funkce stavová, musí platit, že když
,
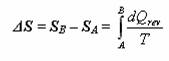pak
.
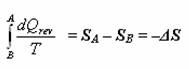Fakt, že platí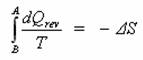 
, dosadíte do vztahu 
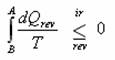, uvedeného o 9 řádků výše, vychází vám 
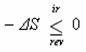a z toho plyne, že
. Protože všechny ireverzibilní (nevratné) děje jsou samovolné, je z tohoto odvozeného vztahu zřejmé, že pokud bude změna entropie větší než nula (ΔS > 0), bude děj probíhat samovolně. Z odvozeného vztahu je také zřejmé, že pro ΔS = 0 v systému probíhají pouze vratné děje a systém je v rovnováze. Pochopitelně pro ΔS < 0 děj neprobíhá samovolně. Z toho je patrné, že entropie je kritériem samovolnosti děje. Možná vám odvození přijde velice dlouhé a složité, ale uvědomte si, že uživatel potřebuje kritérium, ne jeho odvození. Televizi jste schopni také používat, aniž víte, jak vypadá uvnitř, ale pokud vám nefunguje, je výhodou vědět, jak to v ní vypadá. S entropií je to stejné.
Entropie a pravděpodobnost
Představte si pokoj čtrnáctiletého teenegra. V podstatě se může nacházet ve dvou krajních stavech. Zcela a dokonale uklizený (tzn. všechno na svém místě a krásně uspořádané) a nebo zcela „zabordelený“ (tzn. každá část pokoje se může vyskytovat téměř kdekoliv). Ze zkušenosti víte, že druhý stav je podstatně pravděpodobnější. Proč tomu tak vlastně je? Vezměte jednu část pokoje, například pero. Můžete ho umístit kamkoliv, ale jenom jedno místo je to místo, kam patří (kelímek na tužky). Ostatních míst, kde může pero být, je mnohonásobně více (pod stolem, v posteli, v květináči, za oknem, atd.). Právě proto, že těchto míst je více, je tento stav pravděpodobnější. Vztáhnete-li tuto situaci na kteroukoliv věc, která se v pokoji nachází, je zřejmé, že pravděpodobnost, že všechno bude na svém místě oproti pravděpodobnosti, že nebude, je ještě mnohem menší. Z toho plyne, že pravděpodobnost, že bude pokoj uklizený, je podstatně menší, než že je neuklizený. A protože se dějí věci spíše pravděpodobné než nepravděpodobné, je zřejmé, že samovolný bude děj, který bude probíhat ze stavu méně pravděpodobného do stavu více pravděpodobného. Tedy „samovolně“ se z uklizeného pokoje stane neuklizený a ne naopak. Pokud chcete, aby tomu bylo naopak, musíte pokoj uklidit (přenést všechny věci na své místo), ale k tomu už musíte dodat energii, ale pak to není děj samovolný. Určitě cítíte, že to tak nějak je, ale z termodynamického hlediska má tento příklad pár nedostatků, podíváme se tedy na jiný, který je dokonalejší.
Řekněme, že malé dítě má krabičku na lentilky se třemi přihrádkami, které ovšem nedosahují až k víku krabičky, jako je to na obrázku.
krabička na lentilky
Od babičky dostane několik krabiček lentilek (pro jednoduchost obsahující jenom tři barvy – modrá, červená, žlutá). Dítě si je rozdělí do přihrádek podle barev a přiklopí víkem. Chce mamince ukázat, jak si je rozdělilo. Modrá vlevo, červená uprostřed a žlutá vpravo.
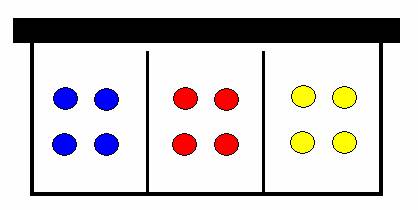
krabička s barevně odlišenými lentilkami
Cestou ale zakopne o autíčko, které předtím neuklidil a všechny lentilky se promísily.
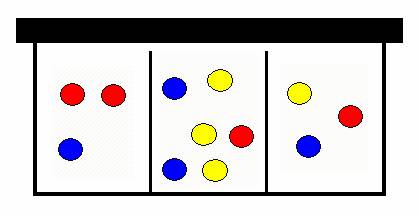
krabička lentilek po prvním zakopnutí
Dítě si řekne: „Když zakopnu ještě jednou, tak se mi určitě promísí zase zpátky“. Zakopne tedy o panenku, kterou neuklidila jeho sestra, ale ouha. Lentilky jsou zase promíchány jinak, ale od původního uspořádání se velice liší.
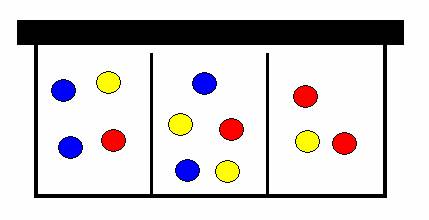
krabička lentilek po druhém zakopnutí
Proč se tedy lentilky nedostaly do původního uspořádání podle barev? No proto, že onen stav, že všechny lentilky jsou uspořádány podle barev, je pouze jeden, zatímco stavů, kdy jsou lentilky promíseny, je velice mnoho. Pokud uděláte mnoho pokusů se zakopnutím (doufáme, že máte dobré zdravotní pojištění), zjistíte, že do původního stavu podle barev se v podstatě nedostanete. Opět tedy děj probíhá samovolně ze stavu méně pravděpodobného do stavu pravděpodobnějšího a nikoliv naopak. Není to nic jiného než zkušenost, ale nikdy se tomu nestalo jinak.
A teď nějaký fyzikální příklad.
Představte si dva plyny, které jsou od sebe odděleny přepážkou.
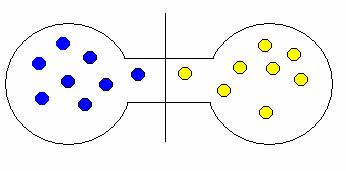
Pokud onu přepážku odstraníte, plyny se samovolně promísí. Proč? Opět stav, kdy jsou oba plyny ve vlastní nádrži je méně pravděpodobný než stav, kdy jsou molekuly nahodile rozmístěny v obou nádržích. Trochu to dokumentují následující obrázky.
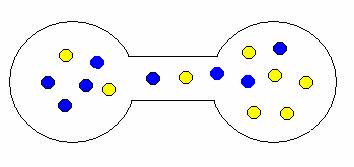
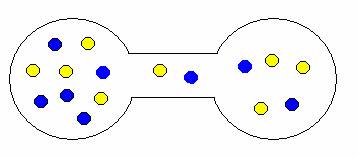
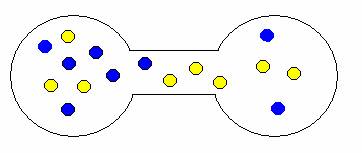
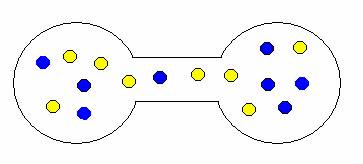
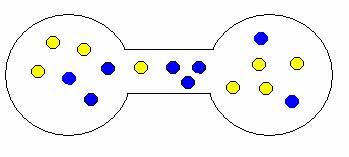
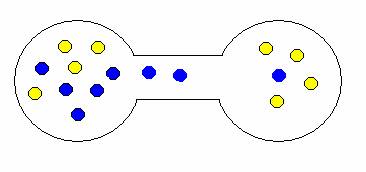
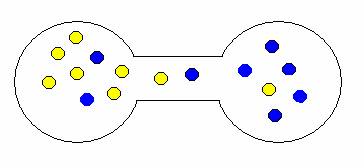
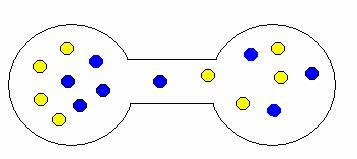
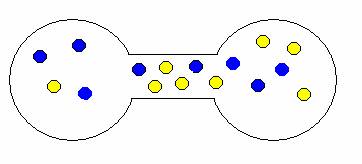
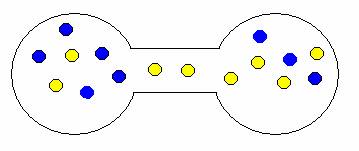
ukázka možných kombinací expanze (mísení) plynů
Je zřejmé, že je-li pravděpodobnost děje kritériem jeho samovolnosti, stejně tak jako entropie, budou mít tyto dvě veličiny asi něco společného. L. E. Boltzman v roce 1896 odvodil, že tomu tak opravdu je, a vztah mezi entropií a pravděpodobností formuloval následovně:
Kde k je Boltzmanova konstanta k = R/NA (R je univerzální plynová konstanta, která má hodnotu 8,314, a NA je Avogadrova konstanta, která nám říká, že 1 mol obsahuje 6,022.1023 částic) a P reprezentuje termodynamickou pravděpodobnost děje (daného uspořádání).
Samovolné děje lze charakterizovat nejen zvětšením entropie, ale též vzrůstem neuspořádanosti vznikajícího stavu soustavy, vzhledem ke stavu výchozímu. Proto se entropie také definuje jako míra neuspořádanosti systému. Čím je systém neuspořádanosti větší, tím má vyšší entropii. Entropie se udává v jednotkách J.mol-1.K-1.
Změna neuspořádanosti systému
Změna neuspořádanosti systému při přeměně: H2O (s) ---> H2O (l)
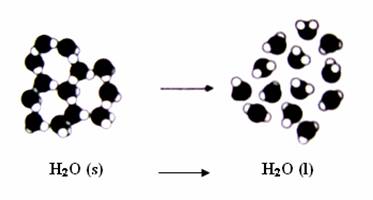
Při tomto ději přechází systém do stavu s větší neuspořádaností, tedy entropie se zvětšuje:
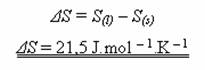
Entropie se zvětší i při přeměně vody ve vodní páru. V kapalném skupenství vody je omezený pohyb molekul, zatímco ve vodní páře se molekuly pohybují chaoticky. Systém přechází do stavu s větší neuspořádaností, tedy i s větší entropií.
Veličina entropie je definována na základě kruhového děje a podle její hodnoty můžete charakterizovat samovolnost daného děje pro izolované soustavy:
samovolný děj ΔS > 0
nesamovolný děj ΔS < 0
Úlohy
Úloha 1:
Vypočítejte teplotu kotle, aby při teplotě okolního vzduchu 302 K, byla účinnost vratného tepelného stroje 0,6?
Úloha 2:
Tepelný stroj pracuje s teplejší zásobníkem o teplotě t2 = 500 °C a chladnějším zásobníkem o teplotě t1 = 140 °C. Pro následující údaje o práci stroje W, teplu vyměněné mezi strojem a chladnějším zásobníkem Qchlad a teplu, vyměněné mezi strojem a teplejším zásobníkem Qtepl zjistěte charakter děje ve stroji a rozhodněte, zdali jsou uvedená data ve shodě s I. a II. větou termodynamiky. Údaje:
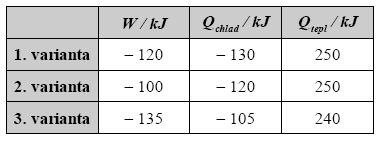
Úloha 3:
Vypočítejte, při které z teplot
a) 280 K
b) 480 K
c) při obou teplotách
d) při žádné z uvedených teplot
bude reakce 
probíhat ve směru zleva doprava za předpokladu, že ΔH a ΔS nezávisí na teplotě. 
Úloha 4:
Vysvětlete, proč při pražení rumělky (cinabaritu, HgS) nevzniká jako konečný produkt oxidu rtuťnatý, když pražením rud většinou vznikají oxidy kovů? Máte-li k dispozici následující údaje: ΔS = 0,18 kJ.mol-1, ΔH = 181,4 kJ.mol-1.
Nápověda: oxid rtuťnatý je nestabilní.
