Vnitřní energie
Jistě se všichni nedočkavě těšíte na první větu termodynamiky 
. Ale než se k ní dostanete, musíme ještě zavést novou veličinu – vnitřní energii U.
Probíhá druhý poločas finálového utkání Ligy mistrů mezi týmy Bayern Mnichov a Chelsea. Petr Čech chytá tutovku Balacka. Bere míč do rukou a vykopává ho na vybíhajícího Drogbu. Při výkopu se míč ocitá ve výšce h, přičemž letí rychlostí v.
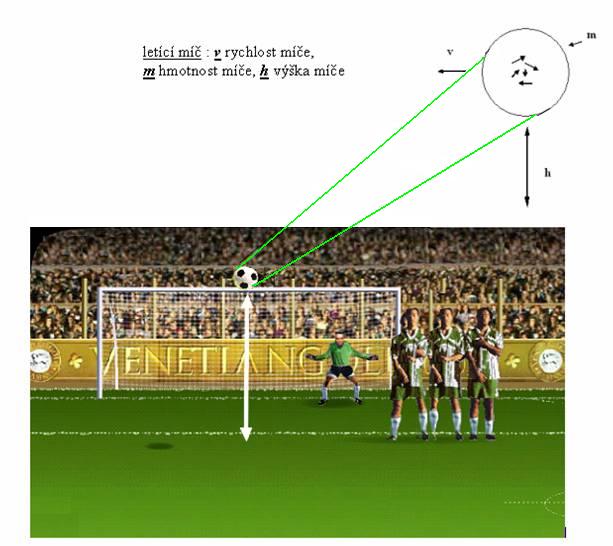
Pokuste se nyní určit celkovou energii míče. Vzhledem k tomu, že je míč ve výšce h nad zemským povrchem, má potenciální energii Ep (Ep = m.g.h). Dále letí rychlostí v, má tedy kinetickou (pohybovou) energii Ek 
. Ale to není vše!
V míči je také vzduch, konkrétně molekuly a atomy, ze kterých je vzduch složen (tedy O2, N2, CO2, Ar atd.). Ty se rovněž pohybují (nezávisle na pohybu míče), tedy mají také kinetickou energii Ek,m, kterou je třeba do celkové energie míče také zahrnout.
Dále na sebe molekuly navzájem působí van der Waalsovými silami. Energie vyplývající z těchto interakcí se nazývá také potenciální energie Ep,m, nicméně nesmíte ji zaměňovat s potenciální energií tělesa Ep (v našem případě míče). Dále byste měli přičíst energii elektronů a jader atomů tvořících molekuly, energii chemických vazeb, atd., vlastně veškeré energie všech částic nacházejících jak v míči, tak v jeho obalu. A právě součet všech těchto energií, kromě potenciální energie Ep a kinetické energie Ek míče, je naše vnitřní energie.
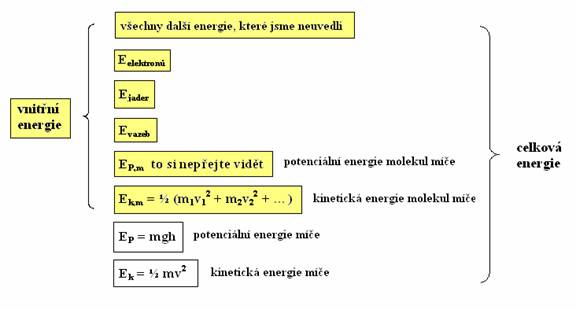
ukázka některých energií přispívajících k celkové energii míče
Uvedeme si další, možná trochu neumělý, ale možná snáze pochopitelný příklad na objasnění pojmu vnitřní energie. Představte si letadlo, v němž se nacházejí cestující. Letadlo letí v nějaké výšce a pohybuje se určitou rychlostí. Lidé v letadle se mohou libovolně a chaoticky pohybovat nezávisle na rychlosti letadla. Tedy vše, co se děje uvnitř letadla, můžete chápat jako vnitřní energii letadla.
ukázka některých energií přispívajících k celkové energii letadla
Vnitřní energie soustavy je obecně souhrnem všech druhů energií, které existují v izolované soustavě (v našem případě míči, letadle). Patří mezi stavové veličiny. Nyní se nabízí otázka :
Jakým způsobem lze ovlivňovat vnitřní energii?
Jakým způsobem lze ovlivňovat vnitřní energii
Snížíte-li teplotu soustavy, molekuly soustavy se budou pohybovat pomaleji. Sníží se tedy jejich kinetická energie a musí dojít i ke změně vnitřní energie. Při zvýšení teploty soustavy je tomu naopak.
Zvětšíte-li objem soustavy, molekuly budou dál od sebe a budou na sebe méně působit. Tím se změní jejich potenciální energie a musí dojít i ke změně vnitřní energie. Při snížení objemu je tomu naopak.
Protože platí zákon zachování energie, tak se tato vnitřní energie nemůže nikam ztratit. Tedy přejde do okolí anebo z okolí, obvykle ve formě tepla nebo práce, jak budeme ještě podrobně probírat v dalších kapitolách, nebo přejde jedna v druhou (např. kinetická energie molekul v potenciální energii molekul a naopak).
Matematická formulace 1. věty termodynamiky
příklad porušení 1. věty termodynamiky – z „ničeho“ vzniká „něco“ – v našem případě lidé
Hurá. Už víte, co je vnitřní energie. Takže ke znění 1. věty termodynamiky. Toto znění má neobyčejné kouzlo, neboť je velmi jednoduché a nebude vám trvat dlouho, než se ho naučíte. Matematická formulace této věty vypadá následovně.
Vyjádřeno slovy změna vnitřní energie soustavy se rovná součtu práce W, kterou vykonají okolní tělesa působící na soustavu, a tepla Q, které soustava od okolí přijme.
Důkaz nečekejte, protože 1. věta termodynamiky je axiom. Tzn. nikdo nikdy nepozoroval, že by se vnitřní energie systému změnila jinak, než výměnou práce nebo tepla.
Jelikož teplo a práce jsou druhy energie (všimněte si, že jednotky obou jsou Joule – J ), je zřejmé, že 1. zákon termodynamiky je vlastně zvláštním případem zákona zachování energie. Pokud se budete chtít vrhnout rovnou do výpočtů, bude nezbytné určit znaménka pro práci a teplo, které soustava vymění s okolím. V podstatě je jedno, které znaménko přiřadíte konkrétnímu ději, pokud tento systém zachováváte během celého výpočtu a správně interpretujete, nicméně, po letech sporů se však ujala následující konvence.
vývoj znaménkové konvence
Pokud systém práci přijme, je znaménko kladné. Pokud vykoná, je znaménko záporné.
soustava přijme práci |
W > 0 |
soustava vykoná práci |
W < 0 |
soustava přijme teplo |
Q > 0 |
soustava odevzdá teplo |
Q < 0 |
V případě, že systém nevyměňuje s okolím teplo, již tak jednoduchá 1. věta termodynamiky se dále zjednodušuje na následující tvar.
- Jestliže se teplo Q = 0, jedná se o adiabatický děj a podle 1. termodynamického zákona: ΔU = W.
Je to děj, při kterém nedochází k tepelné výměně mezi soustavou a okolím. Tzn., že systém např. koná práci pouze na úkor vnitřní energie, a tím pádem se musí ochlazovat.
- Pokud systém nekoná, popřípadě nepřijímá práci, W = 0, pak je změna vnitřní energie rovna teplu a podle 1. termodynamického zákona: ΔU = Q
Teplo a práce nejsou stavovými veličinami. Podíváme se, proč práce není stavovou funkcí. Znovu se podíváme na příklad s nejvyšší horou České republiky. Budete uvažovat práci vrtulníku. V prvním případě vrtulník vykoná práci spojenou na výstup hory. Tedy poletí přímo. V druhém případě vrtulník vystoupá do určité výšky a poté bude klesat na horu. Z tohoto příkladu je zřejmé, že ve druhém případě musel vrtulník vykonat více práce (což je spojeno i s vyšší spotřebou paliva), ačkoliv jeho počáteční i konečný stav je v obou případech stejný.
Teplo (na rozdíl od teploty) také obecně není stavovou funkcí. Opět se vrátíme k příkladu o tělesu s určitou teplotou. Máte k dispozici těleso o teplotě 5°C. Chcete získat těleso s teplotou 20°C. Máte několik možností, jak to provést. Těleso rovnou ohřejete na požadovanou teplotu, k čemuž potřebujete dodat energii, například ve formě tepla. Nebo ho ohřejete na 30°C a necháte zchladnout na 20°C. K tomu bude zjevně potřeba více tepla než v případě prvním. Ačkoliv výchozí i konečný stav je v obou případech stejný, v druhém případě bylo dodáno více tepla než v případě prvním. Teplo tedy není stavovou veličinou. Teplota je stavovou veličinou, protože v obou dvou případech má počáteční i konečný stav stejnou teplotu, ačkoliv jste k němu došli jinou cestou.
Úlohy
Trocha teorie, která je nutná pro výpočet příkladů.
Tepelná kapacita C je v podstatě číslo, které říká, jaké množství tepla musíme soustavě dodat, aby se teplota soustavy zvýšila o 1 K (resp. 1 °C)
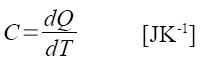
tepelná kapacita při stálém tlaku a objemu vztažená na jeden mol
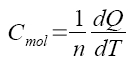
Rozdělení kapacit podle podmínek:
pro ideální plyn
-
nezávisí na objemu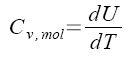
-
nezávisí na tlaku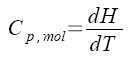 
Mayerův vztah 
udává vztah tepelných kapacit při konstatním tlaku a konstatním objemu za jednotkového látkového množství.
Pro ideální monoatomický plyn platí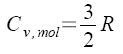 
, tedy Cv,mol je konstantní
Následující vztahy jsou nutné k dalším výpočtům
izotermický děj
a) reverzibilní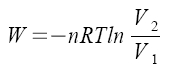 
, 
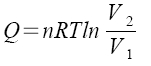
b) ireverzibilní 
izochorický děj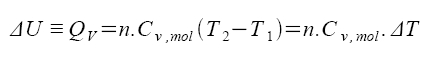 
izobarický děj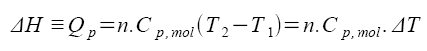 
adiabatický děj 
kde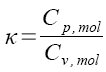 
je Poissonův koeficient
Termodynamický pták (= čínský ptáček)
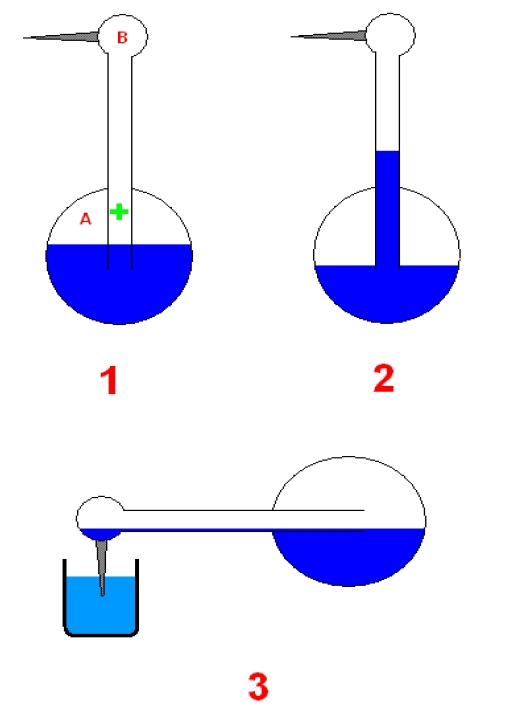
Tato hračka, "čínský ptáček" je tvořena skleněnou baňkou - tělem, na níž navazuje skleněná trubička - krček - zakončená trochu širší hlavičkou (obr. 1). Celý ptáček je uchycen tak, aby se mohl volně otáček okolo osy vyznačené zeleným křížkem. V těle ptáčka je těkavá kapalina, ether, nad kapalinou je jak v těle (A), tak i v krčku a hlavičce (B) sytá pára této kapaliny. Jakmile ptáčkovi vodou smočíme zobáček, dojde vlivem odpařování vody ze zobáčku k ochlazování hlavičky a v hlavičce a krčku spolu s teplotou poklesne i tlak sytých par, zatímco v tělíčku zůstává tlak stále stejný. Tento rozdíl tlaků vytlačuje kapalinu z tělíčka do krčku (obr. 2). Spolu s přesouvající se kapalinou se pomalu přesouvá i těžiště celého ptáčka. Vystoupá-li kapalina dostatečně vysoko, ptáček se převáží a nakloní dopředu. Když se nakloní dostatečně (obr. 3), dojde k propojení tělíčka a hlavičky, tlaky se vyrovnají, kapalina přeteče zpět do tělíčka a ptáček se opět napřímí (opět obr. 1). Při předklonu si ale ptáček smočil zobáček ve skleničce s vodou, která stojí před ním, takže se voda z jeho zobáčku zase začne odpařovat a celé se to může opakovat.
FYZIKÁLNÍ WEB: Čínský ptáček. [online]. [cit. 2008-07-06]. Dostupné z http://fyzweb.cuni.cz/odpovedna/img/cinskyptacek.gif
Úloha 1:
1 mol monoatomického ideálního plynu vykoná reverzibilně následující cyklický děj:
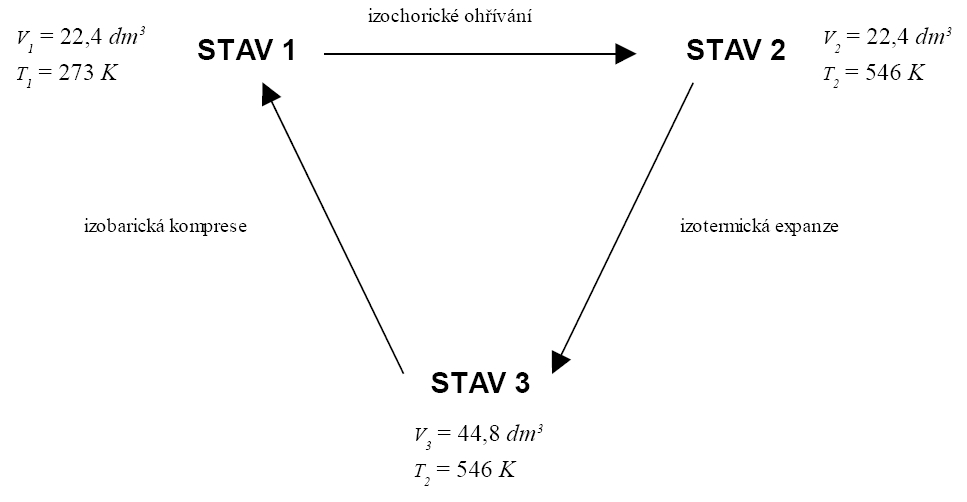
Vypočítejte v jednotlivých stavech vyměněnou práci a teplo a změnu vnitřní energie při jednotlivých dějích.
Úloha 2:
Soustava obsahující 1 mol ideálního plynu vykonala reverzibilní izotermickou expanzi, při níž zvětšila svůj objem desekrát. Vykonala při tom práci 7140 J. Počáteční tlak v soustavě byl 101,3 kPa. Vypočítejte teplotu T a počáteční objem V1 soustavy.
Úloha 3:
Při teplotě 18 °C expanduje 1 mol ideálního plynu z objemu 3 dm3 na objem 10 dm3 a pak je opět zkomprimován na původní objem. Je-li tento děj proveden izotermicky a reverzibilně, spočtěte objemovou práci při expanzi a při kompresi.
Úloha 4:
Uvažujte proces popsaný v úloze 3 s tím, že expanze bude provedena ireverzibilně v prvním kroku a zpětná komprese bude provedena opět ireverzibilně v jednom kroku na tlak odpovídající konečnému objemu 3 dm3. Určete objemovou práci při takto provedené expanzi a kompresi.
Úloha 5:
K ohřátí 100 g methanu z 15 °C na 22,5 °C při konstatním tlaku je zapotřebí právě 0,5 Wh. Vypočtěte molární tepelnou kapacitu Cp,mol methanu za předpokladu, že Cp,mol je v daném teplotním rozmezí konstantní. Molární hmotnost methanu uvažujte 16,04 g.mol-1.
Nápověda: 1 Wh = 3600 J.
Úloha 6:
V objemu 1 dm3 je při 20 °C 1 mol ideálního plynu. Porovnejte práci, kterou plyn vykoná při izotermické reverzibilní expanzi na konečný objem 3 dm3, s prací vykonanou při ireverzibilní izotermické expanzi proti konstatnímu vnějšímu tlaku na stejný konečný objem, tedy 3 dm3.
Úloha 7:
3 moly ideálního plynu měly na počátku teplotu 200 K a tlak 2 atm. Poté byly reverzibilně adiabaticky stlačeny. Konečná teplota byla 250 K. Molární tepelná kapacita daného plynu při konstantním objemu činí 27,5 JK-1mol-1 a v daném oboru teplot nezávisí na teplotě. Vypočítejte konečný objem a tlak soustavy.