Soustava, systém
Nebudeme se zatěžovat složitými definicemi a za systém budeme považovat tu část prostoru, která je v dané chvíli zájmem našeho studia. Příklad z praxe: Máte budovu plnou pokojů. Pokud vás zajímá, jak si vyměňuje teplo s okolím budova (třeba proto, abyste utratili co nejméně za topení), systémem pro vás bude celá budova. Pokud vás bude zajímat výměna tepla našeho pokoje v této budově (třeba abyste utratili co nejméně za topení, ale účet vašeho souseda vás nezajímá), pak je pro vás systémem váš pokoj. Zbytek budovy se pak stává součástí okolí.
Soustava má obvykle hmotnou náplň. Intuitivně si představíte, že hmota je něco, co můžete uchopit do rukou. To však není docela přesné. Důležité je, že systém je složen z hmotných částic (atomů, molekul, iontů, apod.). Například vzduch je hmotou, neboť se skládá z molekul dusíku a kyslíku (a dalších molekul) a ty jsou také hmotné. Ostatně jakou umí nadělat paseku, když se z nich stane vichřice, tornádo nebo něco horšího.
ukázka ničivé síly tornáda
ukázka oblasti postižené tornádem
Hmotou tedy můžete rozumět i vzduch v místnosti, páru z horkého čaje, kouř z cigaret. Nebo chemii bližší soustavy jako jsou chlór v kádince, vodík ve zkumavce, kyslík v baňce, led na stole, nasycený roztok chloridu sodného.
Víte, co je systém a hmota. Dále zavádíme pojem okolí. Co je to vlastně okolí? Odpověď je možná jednodušší, něž jste čekali. Okolí je vše, co není systém!
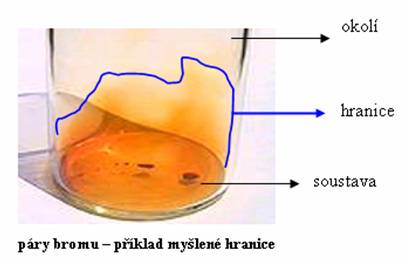
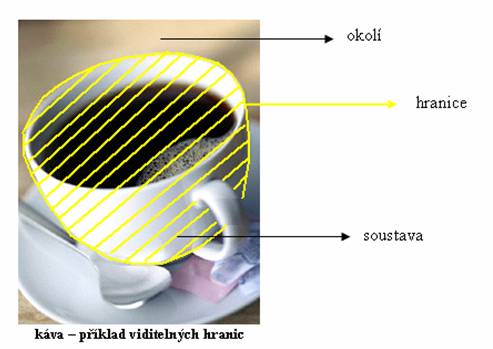
Samozřejmě se ihned nabízí otázka: „Co je mezi soustavou a okolím? “ Mezi soustavou a okolím se nachází hranice. Příkladem může být vodík uzavřený v baňce. Hranice jsou pak stěny baňky. Hranicí také může být (pro nás trochu nepochopitelné) neviditelná (myšlená) stěna. Například páry bromu v kádince. Kouř, který uniká, vytvoří oblak. Budete-li chtít, onen oblak je pro nás systémem a okraje oblaku hranicí.
Nyní se podíváme na myšlené hranice trochu podrobněji. Představte si, že máte oblíbený ušák, ze kterého se díváte na televizi. Přirozeně se chcete dívat z tepla, takže se budete snažit nastavit kamna tak, abyste v ušáku a jeho blízkém okolí měli optimální teplotu. Pokud na to půjdete z termodynamického hlediska, vymezíte si určitý prostor okolo ušáku, v němž se určitě při sledování vašeho oblíbeného pořadu budete nacházet (například krychle o délce hrany 2 m), která bude vaším systémem. Jak je patrné, hranice jsou v tomto případě neviditelné a jsou tvořeny stěnami krychle. Podobný přístup lze aplikovat na oblíbené křeslo svého nepřítele, když se různá teplometná zařízení pokoušíte nastavit tak, aby ve vymezeném prostoru bylo co nejchladněji. Z toho je patrné, že termodynamika je skutečně praktická věda 
.
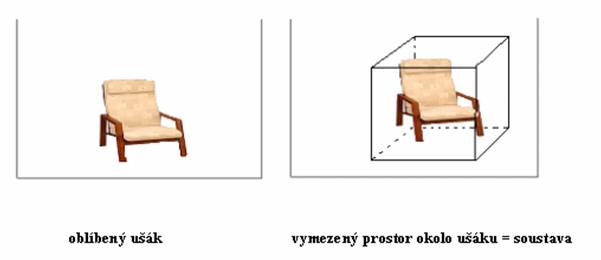
Soustava může být trojího druhu. Otevřená, uzavřená nebo izolovaná. Nyní se podíváme na širší charakteristiku jednotlivých soustav.
Jestliže hranice dovoluje výměnu hmoty i energie mezi soustavou a okolím, označujeme tuto soustavu jako soustavu otevřenou. Příkladem může být již zmiňovaný kouř, vzduch v baňce, ale také hrníček s horkým čajem. Z hrníčku unikají páry a ty jsou složeny z molekul vody, které jsou také hmotnými částicemi. Každý živý organismus je otevřeným systémem, protože k udržení života potřebuje přísun hmoty i energie z okolí, stejně jako energii a hmotu předávat do okolí.
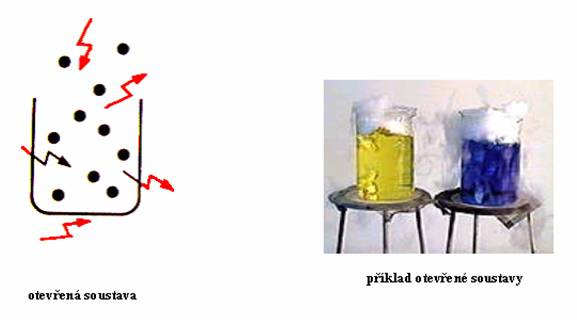
Může-li přes stěny soustavy prostupovat pouze energie a hmota nikoliv, jedná se o soustavu uzavřenou. Například hrníček s teplým čajem přikrytý pokličkou. Energie bude přecházet přes stěny nádoby a po chvíli zjistíte, že hrníček je studený. Ale čaje neubylo. Vyměňovala se pouze energie (teplo), ale čaj (naštěstí) ne, pokud tedy k čaji přijdete za tři hodiny, bude studený, ale hrníček nebude prázdný.
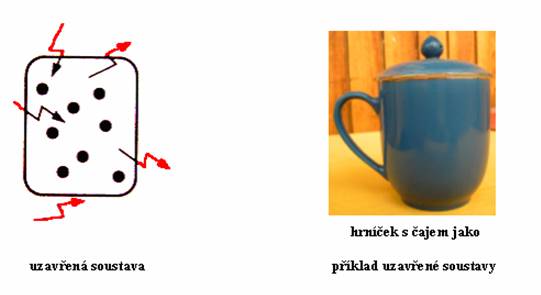
Pokud nedochází k výměně hmoty ani energie s okolím, hovoříme o soustavě izolované. Příkladem je termoska, která udržuje jak teplo, tak i chlad.
Samozřejmě všechny příklady jsou trochu zidealizované. I termoska po čase vymění teplo s okolím. Ale takhle v tom máme pořádek, a to je někdy k nezaplacení.
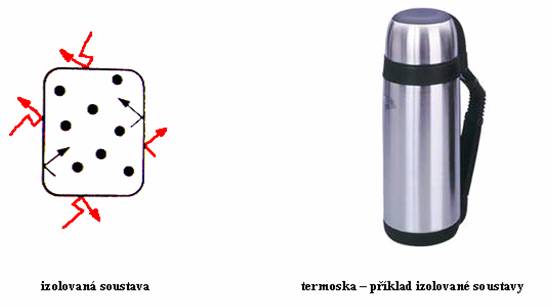
Veličiny popisující aktuální stav soustavy (v daném okamžiku) se označující jako stavové. Mezi stavové veličiny patří například teplota t, termodynamická teplota T, objem V, chemické složení soustavy, látkové množství částic v soustavě n. Stavové veličiny mají takovou zvláštní a pro nás důležitou vlastnost, a to, že jsou závislé pouze na počátečním a konečném stavu soustavy, nikoli však na cestě, kterou soustava prošla. Stavovou změnou pak může být prakticky jakýkoliv děj, při němž se změní stavová veličina. Vysvětleme si to na jednoduchém příkladě. Vzhled auta. Pro názornost si představte, že máte auto po havárii, to většinou nevypadá dobře.
auto po havárii (nespisovně tomu říkáme, že je „hnusné“)
Chcete jej nechat opravit a přestříkat. Tedy odvezete auto do servisu a necháte ho tam. Za několik dní si pro něj přijdete. Vaše auto má nový lak a vypadá jako nové. Vás nezajímá, jak to mechanici udělali. Trvalo-li jim to dlouho nebo krátce, jestli se nadřeli nebo ne, kolik spotřebovali materiálu atd.
Ale důležitější je, že máte auto jako nové. Vzhled vozu tak bude stavovou veličinou (naneštěstí stavovou veličinou nebude, kolik za opravu zaplatíme. Tam už záleží na mnoha okolnostech, například je-li mechanik poctivý nebo ne, jestli se nadřel atd.).
auto jako nové
Příklad z jiného soudku. Máte k dispozici těleso o teplotě 5°C. Chcete získat těleso o teplotě 20°C. Máte několik možností, jak to provést. Těleso rovnou ohřejete na požadovanou teplotu nebo ho ohřejete na 30°C a necháte zchladnout na 20°C. Není důležitá cesta, neboli jak jste to provedli, ale zajímá vás výsledek. V tomto případě těleso o teplotě 20°C. Tedy změna teploty je v obou případech stejná, a to 15°C, přestože ve druhém případě jste spotřebovali více energie než v případě prvním. Teplota je zjevně stavovou veličinou, ale energie (v tomto případě) nikoliv.
Nejvyšší horou České republiky je Sněžka měřící 1602 m. Chtěli byste zdolat její vrchol. Buď přímo vylezete na horu, nebo se můžete nechat dopravit vrtulníkem do výšky například 2800 m, a poté budete klesat k jejímu vrcholu. Z tohoto příkladu je krásně vidět, že nezáleží, jak zdoláte výšku. Rozdílná je dráha. Tedy urazíte pokaždé jinou vzdálenost. Ale nadmořská výška je stavová veličina, kdežto dráha není.
Některé stavové funkce nelze určit absolutně (neznáme přesnou hodnotu), ale pouze jejich rozdíl (Δ - delta). K nim patří některé termodynamické funkce, jako jsou vnitřní energie U, Gibbsova energie G, enthalpie H, apod. Více se o těchto funkcích dozvíte přečtením dalších kapitol tohoto velice poutavého textu . V této chvíli se zaměříte pouze na fakt, proč nelze jejich hodnotu určit absolutně. Důvodem je, že neznáte jejich nulový stav (tj. stav, kdy je jejich hodnota rovna nule). Pro lepší pochopení vám poslouží následující příklad. Představte si, že se díváte z okna velmi vysokého mrakodrapu. Je tak vysoký, že nedohlédnete na zem. Tzn., že neznáte výšku, v němž se nacházíte, a ani polohu (nulový bod – chodník, mořská hladina, apod.), odkud byste ji mohli měřit. Při pohledu z okna vzdálenost mezi vámi a zemí neurčíte, ale stejně tak nedokážete určit, jak vysoko jsou ostatní okna budovy. Pokud však zvolíte např. právě vaše okno za „určovací“, můžete říci, zda jsou okolní okna výš nebo níž než vy. Zvolíte-li pak jedno patro za jednotku, můžete i říci o kolik.
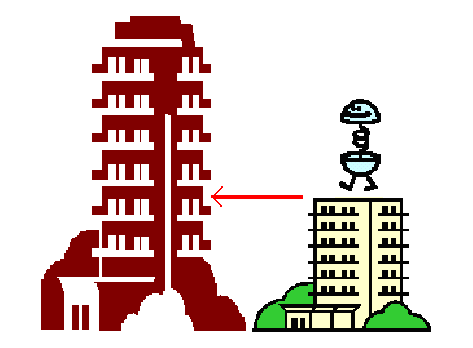
okno označené šipkou mi označuje ono „určovací“
Takže například u vnitřní energie tělesa nemůžete říci, že těleso má vnitřní energii např. 55 kJ, ale můžete říci, že jeho vnitřní energie se změnila například o 2 kJ. Stejně tak jako u zmíněného vysokého mrakodrapu nemůžete říci, že se nacházíte ve výšce například 55 m. Ale můžete říci, že jsme překonali například 2 metry (vylezete-li z jednoho patra do druhého). Ale i to je, jak v následujícím textu uvidíte, důležité.
Veličiny dělíme na extenzivní a intenzivní. Tedy i stavové veličiny můžeme dělit na extenzivní a intenzivní.
Extenzivní veličiny závisí na velikosti systému. Pokud spojíte dvě naprosto totožné soustavy v jednu, zdvojnásobí se hmotnost systému, jeho objem i látkové množství částic v soustavě.
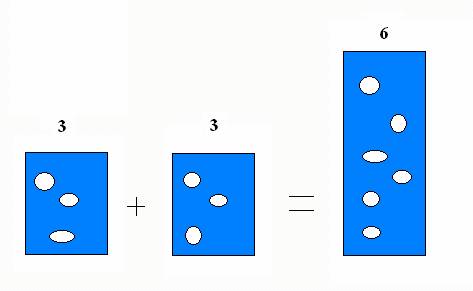
spojení dvou naprosto totožných soustav jako příklad extenzivní veličiny
Ale jak to vypadá s hustotou? Vezměte si dvě sklenice s vodou a smíchejte je dohromady. Opět dostanete vodu. Takže hustota se nebude měnit. Obdobné je to s teplotou a tlakem. Tyto veličiny patří mezi intenzivní stavové veličiny. Intenzivní stavové veličiny se s velikostí systému nemění.
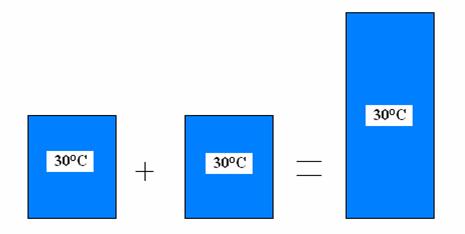
spojení dvou lázní o stejné teplotě jako příklad intenzivní veličiny
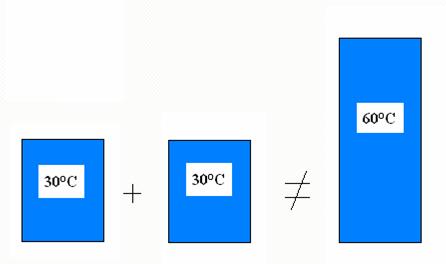
teplota je typickým příkladem intenzivní veličiny
Smísíte-li 1 litr vody o teplotě 30°C a 1 litr vody o stejné teplotě, tak získáte 2 litry vody o teplotě 30°C, ale nikoliv 60°C.
Termodynamický děj
Představte si šálek s čajem, který má teplotu t1. Ohřejete ho na teplotu t2. Tedy soustava přešla ze stavu t1 do stavu t2. Neboli z jednoho stavu do druhého. Tento jev se označuje jako termodynamický děj.
Termodynamický děj může být dvojího druhu. Vratný (reverzibilní) nebo nevratný (ireverzibilní).
Intuitivně chápete, co je to vratný děj a buďte si jisti, že to intuitivně chápete správně. Ale přesto, pár příkladů. Představte si děj, kdy soustava prochází velkým počtem malých stavových změn (rozumíte například mírnou změnou teploty), při kterém je stále v rovnováze s okolím. Tento děj lze kdykoliv zastavit a obráceným sledem malých změn (takže jestliže jste před chvíli teplotu pomalu zvyšovali, teď ji budete snižovat) soustavu vrátit přesně do původního stavu. Takové děje se nazývají vratné = reverzibilní. (Tento příklad není úplně korektní, ale je velmi pochopitelný. Rozpustíte cukr ve vodě. Kdykoliv můžete rozpuštěný cukr přeměnit zpět na pevný pomocí krystalizace.)
Opakem je děj nevratný = ireverzibilní. To jsou takové děje, které jsou provedeny tak, že je sledem zpětných změn stejné velikosti a směru nelze vrátit. Například spálení dřeva na popel. Nevratné děje jsou všechny děje, které probíhají samovolně (tj. bez dodání energie). Dalším příkladem může být oxidace sodíku na vzduchu. Sodík se po vyjmutí z petroleje na vzduchu okamžitě pokrývá bílou vrstvičkou sloučenin kyslíku a sodíku, ale z těchto sloučenin už nikdy samovolně sodík za normálních podmínek nevznikne.
>>nahoru<<
Typy dějů za konstatní hmotnosti
Některé děje probíhají za podmínek, které se vyznačují tím, že některé stavové veličiny jsou při nich konstantní. To pro vás může mít značný význam, například nestavová funkce se může stát stavovou, některé vztahy se mohou zjednodušit , apod.
Základními typy dějů za konstatní hmotnosti jsou tyto:
Izotermický děj je termodynamický děj, při kterém zůstává konstantní teplota (Δt = 0).
Izobarický děj je termodynamický děj, při kterém zůstává konstantní tlak (Δp = 0).
Izochorický děj je termodynamický děj, při kterém zůstává konstantní objem (ΔV = 0).
Adiabatický děj je termodynamický děj při kterém nedochází k tepelné výměně mezi soustavou a okolím (ΔQ = 0).
Představte si h1 a h2 jako výšky dvou lidí.
Pokud vás zajímá, o kolik je člověk v modrém větší něž člověk v hnědém, zajímá vás v podstatě, jaký je mezi nimi výškový rozdíl. Tedy h2 – h1. Tento rozdíl často značíme jako Δh. Matematicky zapsáno: Δh = h2 – h1.
Podobně můžete používat symbol Δ i u jiných veličin. Například rozdíl vnitřních energií atd.
ΔU = U2 – U1
Další příklad. Máte těleso o teplotě 30°C a ohřejete ho na teplotu 50°C. Teplotní rozdíl je:
Δt = 50°C – 30°C = 20°C
Úloha 1:
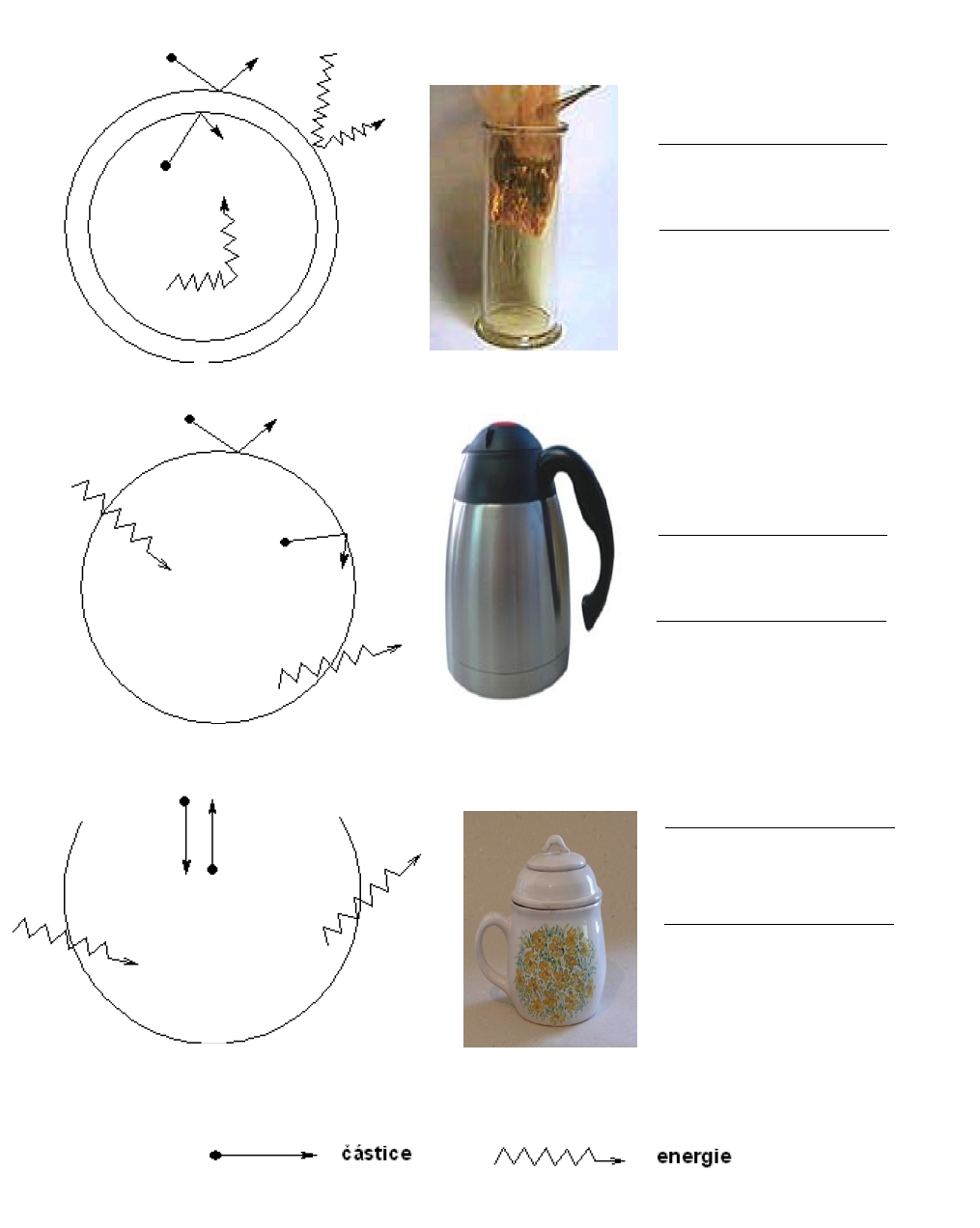
Spojte obrázek vlevo s odpovídajícím obrázkem vpravo a utvoříte dvojice systému, které k sobě logicky patří. Dále připište, o jakou soustavu se jedná a uveďte jeden konkrétní příklad této soustavy v praxi (kromě těch uvedených na obr.).
Pod tabulkou se nacházejí otázky I až III. Vaším úkolem je správně odpovědět na dané otázky, ve kterých může být více správných odpovědí. Poté v následující tabulce vybarvěte vždy příslušné políčko, které odpovídá správné odpovědi (správným odpovědím) dané otázky. Objeví se vám obrázek.
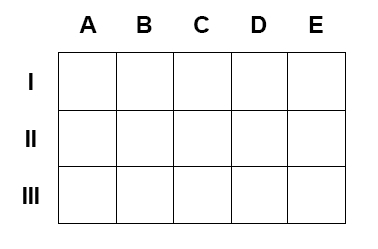
Otázka I:
Termodynamický systém:
a) nemůže měnit svůj objem
b) nemůže s okolím vyměňovat ani hmotu ani energii
c) může s okolím vyměňovat teplo i práci
d) může s okolím vyměňovat jen hmotu
e) může s okolím vyměňovat jen teplo.
Otázka II:
Termodynamické systémy mohou být uzavřené, otevřené, izolované, atp. Nevyměňuje-li systém s okolím hmotu,
může jít o systém
a) otevřený
b) uzavřený
c) izolovaný
nevyměňují-li si energii, musí jít však o systém
d) uzavřený
e) izolovaný
Otázka III:
Jeden Joule je jednotkou energie, která je rovna:
a) 1 Watt na 1 s
b) 1 kPa na 1 dm3
c) 1 kPa na 1 cm3
d) 1 m2.kg.s-2
e) 0,2389 cal
Úloha 3:
V každé větě je ukryt jeden pojem mající něco společného s termodynamikou. Tyto pojmy nalezněte a napište, co o nich víte.
Úloha 4:
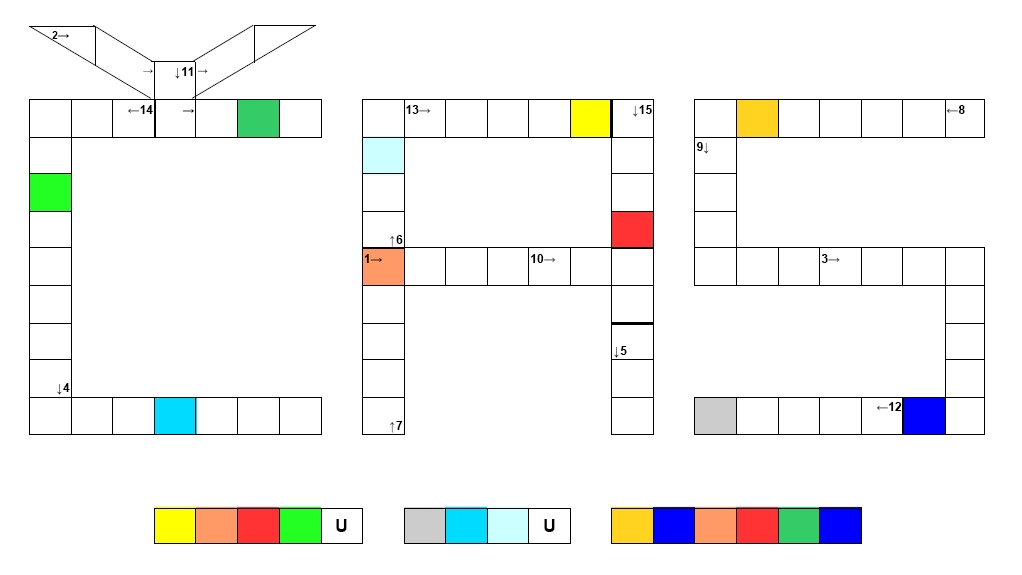
Po vyškrtání všech slov zůstane 27 písmen, která čtena po řádcích tvoří tajenku. Nejdříve odhalte slova skrývající se v křížovce, jejichž stručná charakteristika je zapsána pod osmisměrkou.
Tajenkou osmisměrky je vědní obor zabývající se studiem fyzikálních a chemických dějů spojených s energetickými změnami. Něco nám však říci nemůže, a to za (viz křížovka, která následuje) proběhne
Charakteristika slov pro vyškrtání:
1) je tvrzení, které je ve shodě s naší zkušeností, ale nelze jej dokázat
2) je tvořen dvěma od sebe oddělenými elektrickými náboji opačné polarity
3) veličina, která umožňuje jednoznačně měřit tepelné změny reakcí probíhajících za konstantního tlaku
4) kritérium samovolnosti děje za izotermických podmínek
5) anglický název pro plynnou látku
6) americký vědec, který je autorem kritéria samovolnosti děje za izotermicko – izobarických podmínek
7) obecný výraz pro hmotné částice (atomy, molekuly, ionty atd.)
8) označení tohoto matematického symbolu ∫
9) jeden z autorů 1. termochemického zákona, který má iniciály P.S.L.
10) základní jednotka látkového množství (množné číslo)
11) síla po dráze
12) anglický název pro pevnou látku
13) obecně zařízení, které pracuje za určitých podmínek (např. tepelných)
14) oblast termodynamiky zabývající se studiem tepelného zabarvení chemických reakcí
15) fyzikální veličina, jejíž základní jednotkou je Pascal
16) anglický název pro kapalnou látku
17) část prostoru, která je v dané chvíli zájmem našeho studia z termodynamického hlediska
18) popis aktuálního děje, stejné označení mají také veličiny, mezi které patří například teplota, nadmořská výška
19) přechod systému z jednoho stavu do jiného (např. izotermický, adiabatický)
20) zařízení, které by vyrábělo energii a konalo práci z ničeho
21) německý vědec, který je autorem kritéria samovolnosti děje pro izotermicko – izochorické podmínky
22) množina všech souhlasně orientovaných úseček téže velikosti
Návod: Slova, která odpovídají výše uvedeným charakteristikám doplňte do křížovky vždy tak, jak vyznačuje šipka. Nelekněte se, pokud slovo přesahuje do dalšího číslem označeného pole. Naopak, považujte to za nápovědu. Číslo v křížovce odpovídá číslu charakteristiky. Barevně vyplněná pole tvoří tajenku.
